SEMANA 9
SUCESIONES Y SERIES
-El análisis e convergencia se realiza de igual manera que para el caso de variable real.
-En el caso de variable compleja se presenta el caso de la serie de Laurent que es propia de los números complejos y que no se define para los números reales
SUCESIONES
La sucesión compleja es una función de variables de números naturales en los números complejos.
f:N→C
Los elementos de la sucesión son:
Propiedades
SERIES ESPECIALES
CRITERIOS DE CONVERGENCIA
SERIES DE TAYLOR
Una función analítica admite un desarrollo mediante una serie de Taylor compleja de forma similar a las funciones reales .
Propiedad 1:
Si f es analítica en Z0 , f tiene un desarrollo mediante una serie de Taylor representada por :
Si Z0 =0 entonces la serie toma el nombre de la serie de Maclauri
SERIES DE LAURENT
- En este caso se define ka serie de Laurent que es propia de funciones de variable compleja
- Sea
Sea f:D⊂C→C , función analítica dentro y sobre la frontera de D , entonces:
an,bn
TEOREMA:
Sea f (z) analítica en el anillo r < |z - zo| < R, entonces para todo z en este anillo:
Para n= 0, +/- 1, +/- 2, +/- 3, ... y donde γ es cualquier circunferencia |z - zo|= P ; r < P < R
SEMANA 11
TEOREMA DEL RESIDUO
- En la teoría de los números reales se consideran puntos críticos o aquellos valores que toma la variable x , para los cuales f(x) no se define.
SINGULARIDADES Y POLOS
Se los denomina a todos aquellos valores de "z" donde f(z) no se define
SINGULARIDAD
POLOS:
-Si g(z) es una función analítica en todo el dominio D, siendo D:0<|z−z0|<r y f(z)=g(z)(z−z0)n entonces z0 es un polo de orden "n".
- Se puede demostrar quez0 es un polo de orden "n" si:
limz→z0f(z)=∞
- Se puede demostrar que
RESIDUO:
Si la función f(z) tiene un polo en zj. El residuo de f en zj es a-1 y se calcula mediante:

TEOREMA DEL RESIDUO
Si f(z) es analítica en D, excepto en Z1, Z2, ... , Zj; donde f tiene singularidades. Sea γ una curva cerrada suave o suave por intervalos en D que encierra a Z1, Z2, ... , Zj; entonces:
Jueves 18 de Junio de 2015
EXPOSICIONES GRUPALES
Lunes 22 de Junio de 2015
Funciones periódicas y ortogonales (Grupo 1)
Jueves 25 de Junio de 2015
Coeficientes de Fourier (Grupo 2)
Lunes 29 de Junio de 2015
Funciones pares e impares (Grupo 3)
REFERENCIAS:
- http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C03_Series_Complejas.pdf
- http://www.dma.fi.upm.es/docencia/primerciclo/calculo/Grupo1B/series.pdf









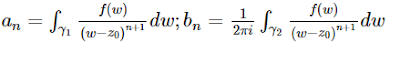


No hay comentarios:
Publicar un comentario