ABRIL

SEMANA 1

NÚMEROS COMPLEJOS

Los números complejos se forman por una parte real y una imaginaria, ya que consta de un factor llamada unidad imaginaria 

Debemos tener en cuenta que:

• Todo número real es Complejo
• No todo numero complejo es número real

Formas de representarlo

Existen varias formas de representarlo pero por el momento solo se explicaran dos tipos:

• Algebraica : z = x + iy ,donde Re(z) = x : Parte real
                                                 Im(z) = y : Parte imaginaria 

                                   

• Rectangular o cartesiana:  z= (x , y)

Hay que tener en cuenta que :

1. Si x = 0 → z = iy  es Imaginario puro
2. Si y = 0 → z = x es  Número real
3. Si x ≠ 0 ^  y ≠ 0 →  z = x + iy Número complejo

Cero complejo:

Si z= x+iy ^ x= 0 ^ y=0 ----> z= 0 + i0 --> z=0 

Opuesto de un complejo:

Si z = x + iy entonces el opuesto de z es: -z = -x - iy

tal que  z + (-z) =  0 + i0

Operaciones con complejos:

Suma:

Sea z1 = x1 + iy1 ^ z2 = x2 + iy2 -----> z1 + z2 = (x1 + x2) + i(y1 + y2)

Propiedades:

• Clausurativa:   Si  z1 ,z2 ∈ C         ---->  z1 +  z2 ∈ C
• Conmutativa:   z1 +  z2 =  z2 +  z1 
• Asociativa:      ( z1 +  z2 ) + z3 = z1 + ( z2  + z3 )
• Existencia del elemento inverso  : Si  z = x + iy   --->  -z = -x - iy
• Existencia del elemento neutro aditivo : Si  z = x + iy ∧ -z = -x - iy   --->  z + ( -z ) = 0 + i0

Multiplicación:

Sean Z1= a+ib ^ z2 =c + di ---->  Z1 · Z2= (a + bi) · (c + di) = (ac− bd) + (ad + bc)i

Nota: Se deben tener en cuenta las principales potencias de la unidad imaginaria como son :  

       i⁰ = 1                 i¹ = i              i² = −1                i³ = −i              i⁴ = 1

Propiedades:

• Clausurativa:  Si  z1 ,z2 ∈ C ---->  z1 . z2 ∈ C
• Conmutativa: z1 .  z2 =  z2 .  z1 
• Asociativa: ( z1 .  z2 ) . z3 = z1 . ( z2  . z3 )
• Existencia del elemento neutro multiplicativo
  
  Sea  z = x + iy ∧ w = a + ib ---->   z . w = ( x + iy )( a + ib )  = x + iy
                                                     z . w = ( xa - yb ) + i( bx + ay )  = x + iy
  
  Resolviendo el sistema de ecuaciones se tiene que: a = 1 ∧ b = 0 -----> w = 1 + i0                                                                                                                      neutro  multiplicativo

• Existencia del conjugado de z                                                                                                                                                                                                                                   Sea   z = x + iy entonces su conjugado es: 

   De modo que Si z. z¯= ( x + iy )( x - iy ) ¯¯¯=x2+y2 es un número Real

•  Existencia del inverso multiplicativo:

• Distributiva:         z1 .  ( z2 + z3 ) =  z1 . z2  + z1 . z3 

Módulo de un Complejo    |z|;∥z∥

                                  

De modo que:

Propiedades:

1. |z| = 0 ---> z = 0
2. |z|≠ 0 ---> |z|> 0
3. |-z| = |z| = |z¯| 
4. |z₁ · z₂| = |z₁| · |z₂|
5. |z₁ / z₂| = |z₁| / |z₂|
6. |z₁ + z₂|= |z₁| + |z₂|

Para tener una idea más clara de lo revisado pueden revisar la siguiente presentación:

Operaciones básicas con Números Complejos from Sabrina Dechima

Webgrafía:

• http://es.wikipedia.org/wiki/N%C3%BAmero_complejo
• http://temasmatematicos.uniandes.edu.co/Complejos/paginas/intro.html}

SEMANA 2

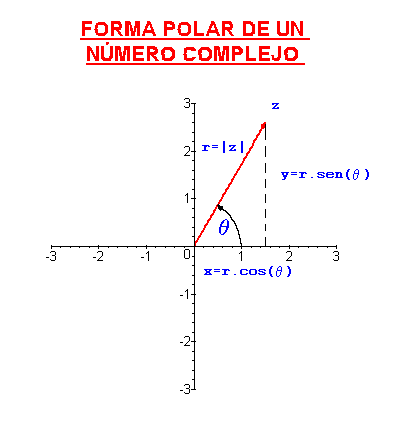
z=  cis(θ1) =cos (θ1)+ i sen (θ1)

                                                r=|z|=((x^2)+(y^2))^1/2   (Módulo)

Multiplicación en forma Trigonométrica:

z1*z2= r1 r2 cis(ʘ1+ʘ2)

 División en forma Trigonométrica:

Sea z1 = r1 cis(θ1) ^ z2 = r cis(θ2)

z1/z2 =[ r1 cis(θ1)] / [r2 cis(θ2)]
z1*z2 =[( r1/r2) cis[(θ1) - (θ2)]

Potenciación:

z^n=r^n[cis(nʘ)]

*Radicación:

z^(1/n)=[(r^1/n)cis[θ+2πk)/n]             ;         k=0,1,2,...,n-1

Nota: El ángulo θ debe estar en radianes

EXPONENCIALES COMPLEJOS

Teorema de Euler:

Forma exponencial de un complejo:

LOGARITMOS COMPLEJOS

En los números complejos solo existen  logaritmos en base e por lo tanto:

log Z = ln Z

Valor Principal     : ln(z) = ln r + iθ 

Valor General:        ln(z) = ln r + i(θ+2πk)


Webgrafía: http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Complejos/marco_complejos.htm

SEMANA 3

• Esta semana realizamos ejercicios de repaso para la prueba 1

Funciones de Variable Compleja

Recordemos que una función real $f$ de variable real sobre un conjunto de números reales es una función que asigna a un número real $x$ ∈D otro número real $y$ = f(x).

Este concepto se generaliza fácilmente al caso complejo:

Una función compleja de variable compleja $f$ definida sobre un conjunto $D$ de números complejos es una función que asigna a cada número complejo $z$ ∈D otro número complejo $w$ = f(z) y la representamos con la notación $f$ : D→ℂ.

La representación gráfica de una función compleja utiliza dos planos complejos, uno para el dominio y otro para la imagen; estos dos planos se pueden representar separados o bien superpuestos (en este último caso, se debe diferenciar de alguna manera el valor del dominio y el de la imagen; por ejemplo, con diferentes colores).

                         

Semana 4

LIMITES DE FUNCIONES DE VARIABLE COMPLEJA

limz←z0f(z)=L↔∀ε>0,∃δ>0/0≤|z−z0|<δ→|f(z)−L|<ε

Propiedades:

limz→z0f(z)=L ∧ limz→z0g(z)=K, entonces:

1. limz→z0[f(z)+g(z)]=limz→z0f(z)+limz→z0g(z)
                               =L+K

2. limz→z0αf(z)=αlimz→z0f(z)=αL;α∈C

3. limz→z0[f(z).g(z)]=limz→z0f(z).limz→z0g(z)
                               =L.K

4. limz→z0[f(z)/g(z)]=limz→z0f(z)/limz→z0g(z)
                               =L/K;K≠0;g(z)≠0

Continuidad 

La función f(z)es continúa en  z0 ssi:

1.   ∃f(z0)
2.  ∃limz←z0f(z)
3. limz←z0f(z)=f(z0)

Nota: Caundo la función no es continua esta puede ser de 2 tipos la primera sera  Discontinua de forma evitable,
 es decir cuando el límite existe por lo que  bastará con redefinir la función en ese punto, o puede ser una discontinuidad
 inevitable ,esto ocurre cuando no existe el límite. 

DERIVADA DE FUNCIONES DE VARIABLE COMPLEJA

Las derivadas de las funciones de variable compleja tienen la misma definición que las derivadas de funciones de variable real, pero hay que tomar en cuenta las definiciones y propiedades de la variable compleja y es importante recordas que  se puede usar las reglas de derivación ya conocidas 

 f(z) es derivable en z0 ssi

                           ∃limz←z0f(z)−f(z0)z−z0                                       o                  ∃limΔz←0f(z+Δz)−f(z)Δz


Propiedades

Ssi ∃f′(z)∧∃g′(z) entonces se cumple que:

1. (f+g)′(z)=f′(z)+g′(z)
2. (αf)′(z)=αf′(z)
3. (f.g)′(z)=f′(z).g′(z)
4. (f/g)′(z)=f′(z)/g′(z);g′(z)≠0

Webgrafía:

http://corcoles.org/uoc/anmat/es/es21.xml
http://www.taringa.net/posts/ciencia-educacion/16436310/Videos-Sobre-Mapeos-Conformes-Variable-Compleja.html